Rikkaat rikastuivat - entä köyhät?
- Tuloerojen kasvun kiistattomin piirre on kaikkein suurituloisimman väestön tulo-osuuden kasvu. Yli puolet heidän bruttotuloistaan oli omaisuus- ja optiotuloja vuonna 2002
- Miten ylimpään prosenttiin päädytään?
- Ylin prosentti kasvatti eniten tulo-osuuttaan
- Tuhannesosa väestöstä sai sadasosan tuloista vuonna 2003
- Ylimmän prosentin tulojen rakenne
- Työsuhdeoptioiden vaikutus tuloeroihin
- Verotus tasaa tuloeroja aiempaa vähemmän
- Palkkaerot eivät selitä tuloerojen kasvua
- Supertähtiteoria
- Mutta kaikkihan saivat lisää kakkua?
- Mitä sitten?
- Lähteet:
- Alaviitteet
Koko dokumentti yhdellä sivulla
Mutta kaikkihan saivat lisää kakkua?
Edellä tuloeroja on tarkasteltu tulo-osuuksien avulla, joten kyse on suhteellisista tuloeroista. Kakkua jaettaessa on pidettävä mielessä, että talouskasvun myötä tulojakauman kaikki kohdat saivat absoluuttisesti suuremman viipaleen vuonna 2003 kuin vuonna 1995.
Kuviossa 3 on esitetty reaalisten mediaanitulojen muutokset vuodesta 1995 vuoteen 2003 koko tulojakauman eri kymmenyksissä. Ylin tulokymmenys on lisäksi jälleen pilkottu pienempiin osiin. Reaalitulot ovat kasvaneet jokaisessa tulojakauman kohdassa, sitä enemmän mitä ylemmäs mennään. Tämä kertoo tietysti suhteellisten tuloerojen kasvusta. Kun suhteelliset tuloerot kasvavat, myös absoluuttiset tuloerot kasvavat.
Tiedämme, että alimman kymmenyksen tulo-osuus aleni 4,5 prosentista 3,8 prosenttiin vuodesta 1995 vuoteen 2003. Ryhmän tulojen keskiarvo oli kuitenkin reaalisesti viisi prosenttia korkeampi vuonna 2003. Koko väestön keskitulo nousi ajanjaksolla yli viidenneksellä. Onko tulotason nousu ollut niin suurta, että se jollakin tavalla kompensoisi pienituloisimpien alentuneita tulo-osuuksia?
Yksi tapa arvioida tulojakaumia siten, että myös tulotason nousu otetaan huomioon, on yksinkertaisesti kertoa tulo-osuudet jakauman keskitulolla. Tuloksena on niin sanottu yleistetty Lorenz-käyrä (Shorrocks, 1983), joka huomioi sekä suhteelliset tuloerot tulo-osuuksien kautta että tulotason nousun keskimääräisten tulojen kautta8. Voimme jopa puhua hyvinvointivertailuista, jos uskomme, että yhteiskunnan hyvinvointi on sen jäsenten tuloista saamien hyötyjen funktio.
Kuvio 3. Reaalitulojen muutos tulokymmenyksittäin ja ylimmässä tulokymmenyksessä vuodesta 1995 vuoteen 2003.
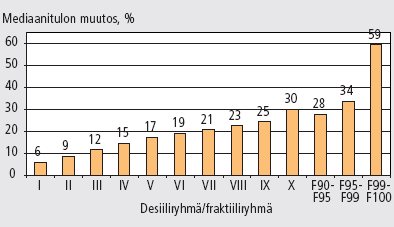
Lähde: Tilastokeskus, tulonjaon kokonaisaineisto
Kuviossa 4 ovat vuosien 1995, 2000 ja 2003 yleistetyt Lorenz-käyrät tulonjakotilaston kokonaisaineistoista laskettuna9. Vaaka-akselilla etenee kumulatiivinen väestöosuus, kuten tavanomaisessa Lorenz-käyrässä. Pystyakselilla on kumulatiivinen tulo-osuus kerrottuna jakauman keskiarvotulolla.
Koko väestön keskiarvotulo voidaan lukea vaaka-akselin kohdasta 100, sillä y-akselin piste on silloin sama kuin keskiarvotulo. Jos tarkastelisimme vain tätä yleistetyn Lorenz-käyrän pistettä, ainoastaan keskiarvotulon muutoksella olisi merkitystä yhteiskunnan hyvinvoinnin kannalta. Jos taas katsoisimme käyriä väestöosuuden ollessa vaikkapa yksi tai kaksi prosenttia, tekisimme päätelmiä vain pienituloisimman väestönosan aseman perusteella. Tässä kiinnostuksen kohteena on koko väestön tilanne, jolloin oleellista on, onko jonkin vuoden yleistetty Lorenz-käyrä aina jonkin toisen vuoden yleistetyn Lorenz-käyrän yläpuolella.
Kuviossa 4 vuoden 2000 yleistetty Lorenz-käyrä on aina vuoden 1995 yleistetyn Lorenz-käyrän yläpuolella. Näin on myös jakauman alaosassa, vaikka kuviosta tätä on vaikea erottaa. Vuoden 2000 jakauma siis dominoi vuoden 1995 jakaumaa, kun kakun kasvu eli keskiarvotulon muutos huomioidaan. Vain suhteellisia tuloeroja tarkastelemalla tilanne on päinvastainen: vuoden 1995 tavanomainen Lorenz-käyrä on koko ajan lähempänä diagonaalia eli dominoi vuoden 2000 Lorenz-käyrää.
Vuoden 2003 yleistetty Lorenz-käyrä puolestaan on vuoden 1995 käyrän yläpuolella kaikkialla muualla, paitsi pienituloisimman kahden prosentin kohdalla. Ero on näissä kohdissa hyvin pieni, mutta käyrät joka tapauksessa risteävät.
Tulosta voi tulkita siten, että yhteiskunnan hyvinvoinnin kannalta keskiarvotulon nousu vuosien 1995-2000 välillä olisi riittänyt kompensoimaan suhteellisten tuloerojen kasvun. Vuotta 2003 vuoteen 1995 verrattaessa vastaavaa päätelmää ei tällä laskentatarkkuudella kyetä tekemään.10
Kuvio 4. Yleistetyt Lorenz-käyrät 1995, 2000 ja 2003.
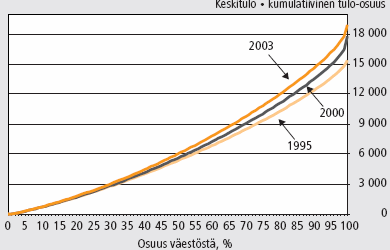
Lähde: Tilastokeskus, tulonjaon kokonaisaineisto
Tulo-osuuksien tai Lorenz-käyrien asemesta informaatio suhteellisista tuloeroista tiivistetään usein yhteen tunnuslukuun. Yleisin on Gini-kerroin, jonka yksi tulkinta on, että se on tasajakoa kuvaavan suoran ja Lorenz-käyrän välinen pinta-ala kerrottuna kahdella. Pienempi pinta-ala eli pienempi Gini-kerroin tarkoittaa tasaisempaa tulonjakoa.
Yleistetyn Lorenz-käyrän tapauksessa käyrän alapuolelle jäävä pinta-ala kuvaa yhteiskunnan hyvinvoinnin kannalta parempaa jakaumaa. Tämä pinta-ala on verrannollinen tunnuslukuun (1-Gini-kerroin) kertaa keskiarvotulo (Sen, 1997). Tämä "Gini-korjattu reaalinen keskiarvotulo" on kasvanut joka vuosi vuosina 1995-2003.
Tulos voidaan tulkita esimerkiksi siten, että suhteellisten tuloerojen kasvun vuoksi hyvinvointi ei ole lisääntynyt samassa suhteessa kuin tulot ovat kasvaneet. Toisaalta talouskasvun vuoksi yhteiskunta voi nykyään kokonaisuutena paremmin kuin kymmenen vuotta sitten, vaikka suhteelliset tuloerot ovat kasvaneet.
Päivitetty 16.6.2006
